Trend Line
Trend line refers to a straight or a curved line that is superimposed on the chart to inform user about direction of the data or the trend, and hence helps in predicting the future values. Due to ability to depict future prices, trend lines are often used in trade analysis to understand the price movement and forecast the value of securities.
In FlexChart, trend lines can be implemented by creating an instance of the TrendLine class. Then, you can set other relevant properties and add it to the Series collection. FlexChart supports regression as well as non-regression trend lines and the fit type and order of these lines can be specified using the FitType and Order property of the TrendLine class, respectively. The FitType property sets one of the following fit types for the trend lines using the FitType enumeration, in the FlexChart control:
| TrendLine.FitType | Snapshot | Description |
|---|---|---|
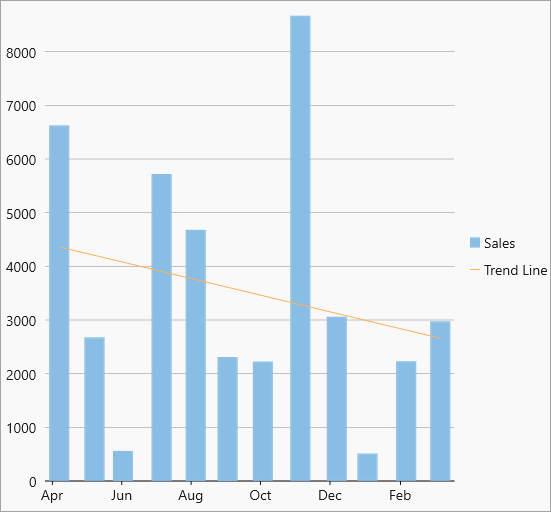
| Linear |  Linear trendline Linear trendline |
A linear trend line is the straight line that most closely approximates the data in the chart. The data is linear, if the data pattern resembles a line. Equation - Y(x) = C0 + C1*x |
| Polynom | 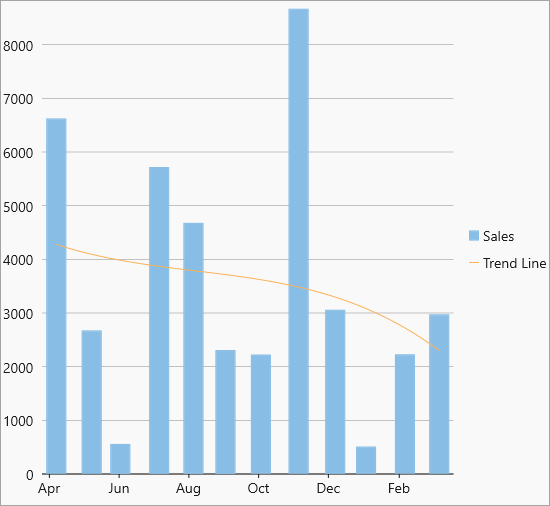 Polynomial trendline Polynomial trendline |
Polynomial trend lines are curved lines that are used with fluctuating data. They are useful for analyzing gains or losses over a large data set. When using a polynomial trend line, it is important to also set the Order of the line, which can be determined by the number of fluctuations in the data. Equation -Y(x) = C0 + C1*x + C2*x2 + : +Cn-1*xn-1 |
| Logarithmic | 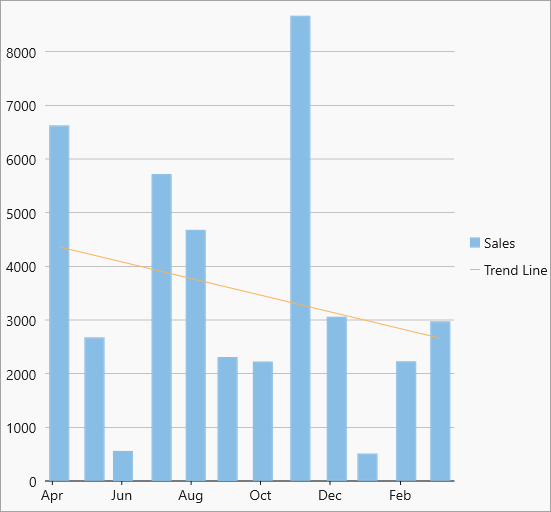 Log trendline Log trendline |
Logarithmic trend line is a best-fit curved line that is most useful when the rate of change in the data increases or decreases quickly and then levels out. A logarithmic trend line can use negative and/or positive values. Equation - Y(x) = C0 * ln(C1*x) |
| Power | 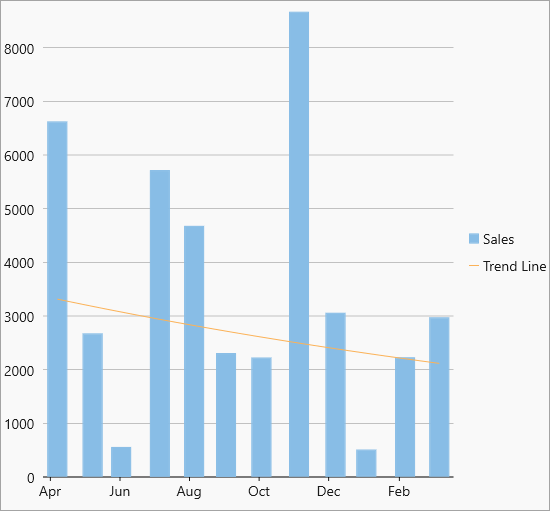 Power trendline Power trendline |
Power trend line is a curved line that is best used with data sets that compare measurements that increase at a specific rate — for example, the acceleration of a race car at one-second intervals. You cannot create a power trend line if your data contains zero or negative values. Equation - Y(x) = C0 * pow(x, C1) |
| Exponent | 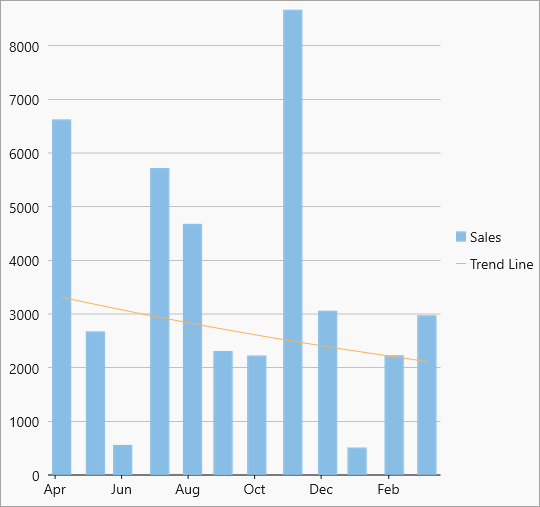 Exponent trendline Exponent trendline |
Exponential trend line is a curved line that is most useful when data values rise or fall at increasingly higher rates. You cannot create an exponential trend line if your data contains zero or negative values. Equation - Y(x) = C0 * exp( C1*x) |
| Fourier | 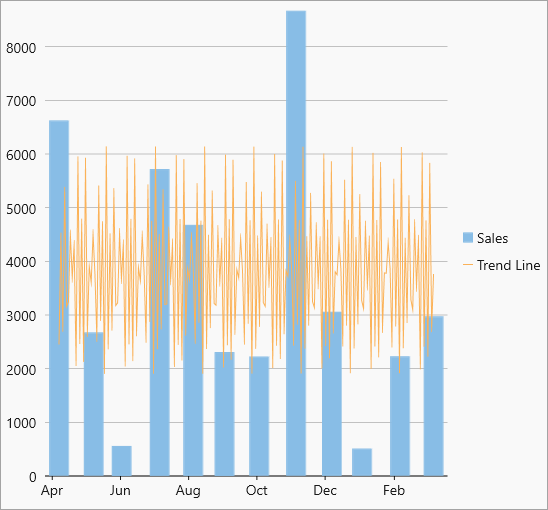 Fourier trendline Fourier trendline |
Fourier trend line identifies patterns or cycles in a series data set. It removes the effects of trends or other complicating factors from the data set, thereby providing a good estimate of the direction that the data under analysis will take in the future. Equation - Y(x) = C0 + C1 * cos(x) + C2 * sin(x) + C3 * cos(2*x) + C4 * sin(2*x) +... |
| MinX | 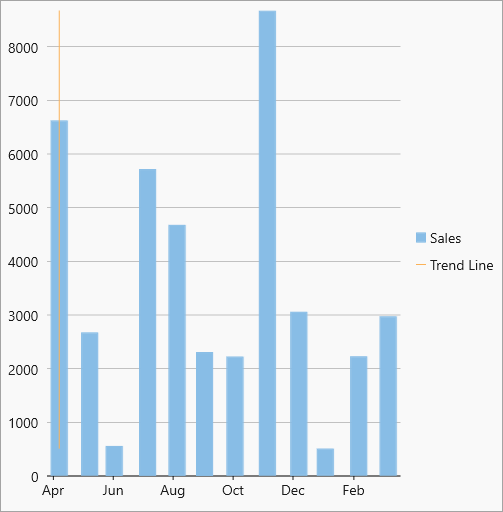 MinX trendline MinX trendline |
The minimum X-value on the chart. |
| MinY | 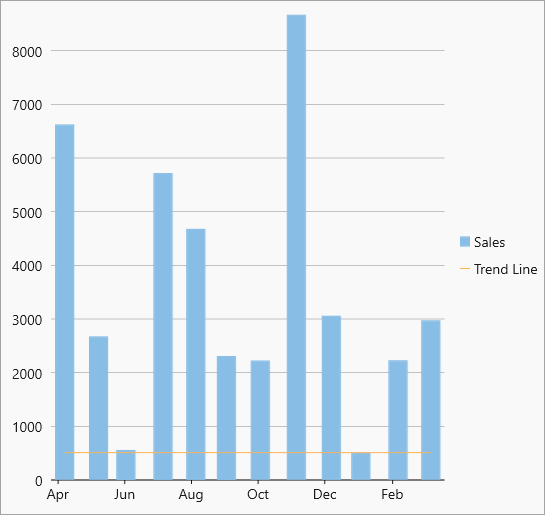 MinY trendline MinY trendline |
The minimum Y-value on the chart. |
| MaxX | 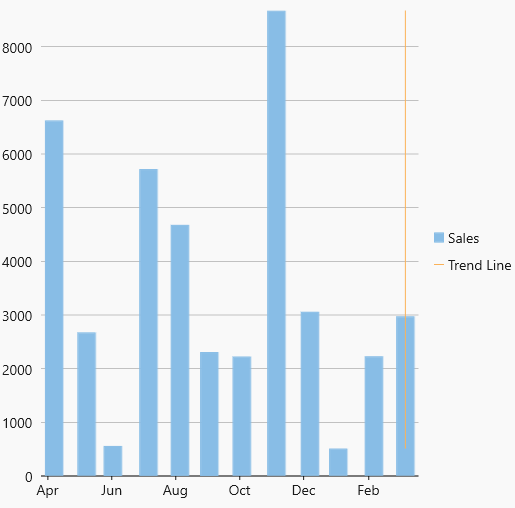 MaxX Trendline MaxX Trendline |
The maximum X-value on the chart. |
| MaxY | 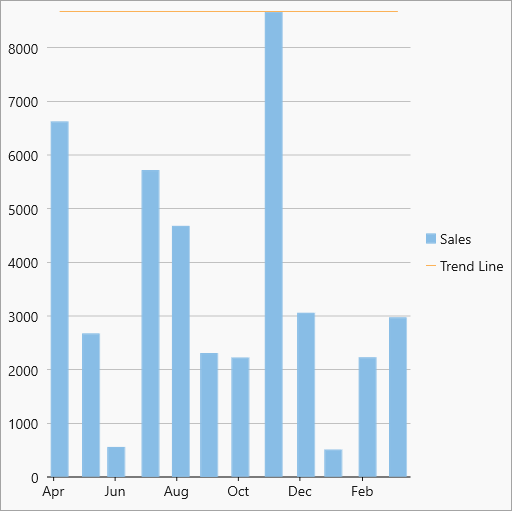 MaxY Trendline MaxY Trendline |
The maximum Y-value on the chart. |
| AverageX | 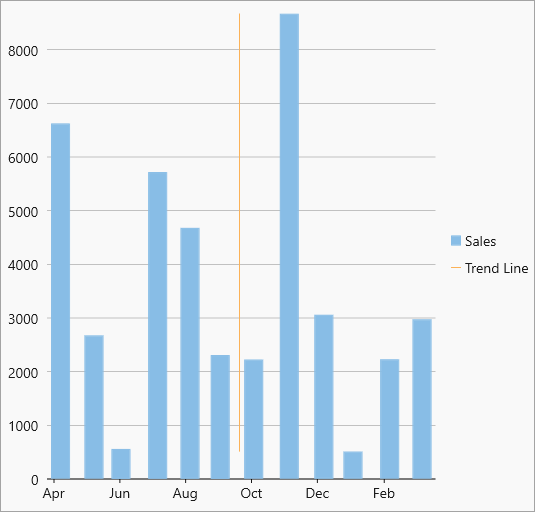 AverageX trendline AverageX trendline |
The average X-value on the chart. |
| AverageY | 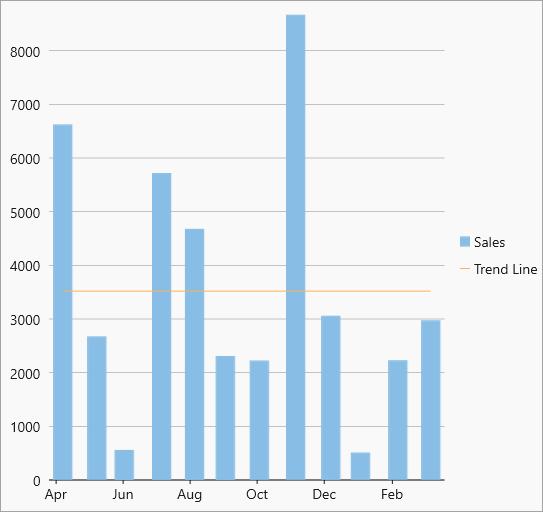 AverageY trendline AverageY trendline |
The average Y-value on the chart. |
The following code showcases trendlines used in charts. This sample uses the same datasource as used in Quick Start.
C1.WinUI.Chart.TrendLine _trendLine = new C1.WinUI.Chart.TrendLine();
_trendLine.SeriesName = "Trend Line";
_trendLine.Binding = "Revenue";
_trendLine.Order = 4;
_trendLine.FitType = FitType.Linear;
flexChart.Series.Add(_trendLine);
Additionally, statistical information about a trend line is crucial for understanding how well the trend line fits the data for making the informed predictions. In FlexChart, the GetRegressionStatistics method retrieves the statistical information about the regression and the RegressionStatistics class contains the main characteristics of regression which can be accessed using the following properties.
| Option | Description |
|---|---|
| Sse | Retrieves the sum of squares error (SSE) also known as residual sum of squares (RSS). |
| Ssr | Retrieves the sum of squares due to regression (SSR) also known as explained sum of squares (ESS). |
| StandardError | Retrieves the standard error for the y estimate. |
| Rsq | Retrieves R squared (coefficient of determination). |
| DegreesOfFreedom | Retrieves the degrees of freedom. |
| Fstat | Retrieves the F statistic, or the F-observed value. |
The following code illustrates the use of GetRegressionStatistics method to retrieve information about standard error for a particular trend line:
private async void ShowRegButton_Click(object sender, RoutedEventArgs e)
{
RegressionStatistics rs = _trendLine.GetRegressionStatistics();
double er = rs.StandardError;
ContentDialog messageDialog1 = new ContentDialog //MessageBox
{
Content = "The StandardError value is:" + er,
CloseButtonText = "OK"
};
messageDialog1.XamlRoot = this.Content.XamlRoot;
await messageDialog1.ShowAsync();
}
Further, the Y coordinate value can be estimated on the trend line by passing corresponding X coordinate value through Approximate method of TrendLine class. For example, the following code showcases the use of Approximate method to estimate Y coordinate value of a trend line when its X coordinate value is 75.3489:
private async void ShowMessageButton_Click(object sender, RoutedEventArgs e)
{
double val = _trendLine.Approximate(75.3489);
ContentDialog messageDialog = new ContentDialog //MesageBox
{
Content = "The approximate value is:" + val,
CloseButtonText = "OK"
};
messageDialog.XamlRoot = this.Content.XamlRoot;
await messageDialog.ShowAsync();
}


